Bu serinin ilk yazılarında veri bilimine giriş yapıp, veri türlerinden bahsetmiştim. Veri Biliminin olmazsa olmazlarından istatistiği bilmeden de veri biliminde gidilen yollar daha iyi aydınlatılamaz.
İlk önce istatistiğin kısa bir tanımını yapalım. İstatistik kısaca, sahadan gelen veriyi nasıl özetleyeceğimizi, analiz edeceğimizi ve ondan yararlı bilgilerin nasıl çıkarılacağını bize öğretir ve bu şekilde kararlarımızı geliştirmede bize yardımcı olur. İstatistik, ekonomi ve iş dünyasında ve aynı zamanda farklı disiplinlerde de bize daha iyi kararlar verebilmemizi sağlayan bilim dalıdır.
İstatistik bilimindeki teknikleri iyi bilmek, bize makine öğrenmesinde karşımıza çıkan verinin daha iyi anlaşılması ve verinin makine öğrenmesi modellerine uygunluğu gibi konularda çok işe yarayacaktır.
İstatistik bilimi kendi içerisinde farklı teknikler, terimler vs. içerdiği için, farklı başlıklar altında size istatistiğin çeşitlerini anlatmaya çalışacağım. İlk yazıma Betimleyici İstatistik ile başlıyorum.
Betimleyici İstatistik – Descriptive Statistics
Türkçe kaynaklarda betimsel/tanımlayıcı istatistik olarak da geçen Betimleyici İstatistik kısaca, elimizde var olan veriyi çeşitli tekniklerle açıklamamızı ve onu daha iyi anlamamızı sağlar. Veriden çıkan sonuçlar, tablolar veya grafikler halinde çalışmanın sonucunda sunulur. Betimleyici İstatistik teknikleri, elimizdeki veri setinde olan mevcut durumu anlamamızda bize fayda getirir.
İstatistik bilimine başlangıçta bazı terimleri bilmemiz gerekiyor. Bunlardan ilk ikisi, evren ve örneklem. İngilizce isimleriyle; population ve sample. Evren kısaca, araştırmacının ilgilendiği tüm ölçümleri içeren veri setidir. Örneklem ise, evrenin içinden seçilen alt bir veri seti kümesidir. Örnek verecek olursak, bir mağaza zincirinin tüm satış elemanlarının günlük satış adetlerini içeren veri seti evren olurken, bu veri seti içinden seçilen, diyelim ki, sadece 20 satış elamanının yaptığı günlük satış sayısı bizim için örneklemi oluşturur.
Bir üst paragraftaki satış elemanlarının örneği üzerinden betimsel istatistiğin metriklerine giriş yapalım. Mağazanın 20 satış elamanının yaptığı günlük satış sayısı, bu satış sayılarının küçükten büyüğe göre sıralanışını içeren python kodunu ve tabloyu aşağıda bırakıyorum.
import pandas as pd
# 20 satış elamanı için günlük satış sayısı
satıs_list = [9,6,12,10,13,15,16,14,14,16,17,16,24,21,22,18,19,18,20,17]
len(satıs_list) #20
# Satış rakamlarını küçükten büyüğe sırala, listeye at
sorted_list = sorted(satıs_list)
# Dataframe oluşturmak için listeleri dict at
dict_df = {'Günlük Satış':satıs_list, 'Dağılım':sorted_list}
# Dataframe oluştur
df = pd.DataFrame(dict_df)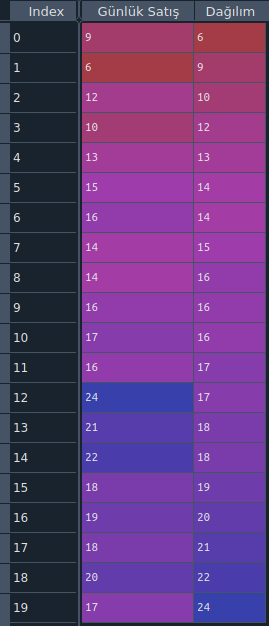
Merkezi Eğilim Metrikleri – Measures of Central Tendency
Median
Veri seti belirli bir düzene göre sıralandığında, eğer veri seti sayısı tekse; ortadaki sayı, eğer veri seti sayısı çiftse; ortadaki iki sayının ortalaması. Yukarıdaki tabloya baktığımızda, Dağılım sütununda, index numarası 9 ve 10 olan iki sayının ortalaması bize Median‘ı verir. Yani 16. Burada dağılım sütununda toplam veri sayısı 20. Dolayısıyla ortadaki iki rakamın ortalamasını aldık. Python Statistics modülünde bulunan median fonksiyonuyla da median sayımızı kolaylıkla bulabiliriz. Aşağıda kodları bulabilirsiniz.
Not: Python‘da median bulmak için, veri setinizi dağılıma tabi tutmanıza gerek yok. Burada dağılım sütunu median metriğini daha iyi anlamak için oluşturuldu.
Mode
Veri setinde en çok tekrar eden veridir. Yukarıdaki tabloda, yine dağılım sütununa baktığımızda en çok tekrar eden verinin 16 olduğunu görebiliriz.
Mean
Bildiğimiz aritmetik ortalama. Bu veri seti için: 317/20 = 15.85
import statistics as st
# Metrik hesaplamaları
st.median(satıs_list) # 16
st.mode(satıs_list) # 16
st.mean(satıs_list) # 15.85Varyans
Veri setindeki her bir terimi ortalamadan teker teker çıkardıktan sonra, çıkan farkların karesini alırız. Ve daha sonra bu değerleri toplayıp veri setinin durumuna göre, veri setinin elaman sayısına veya bir eksiğine böleriz. Çıkan değer bize varyansı verir. Formülle ifade edecek olursak:
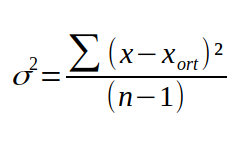
Varyans veri bilimciler için veri setindeki aykırı değerleri görmede büyük kolaylıklar sağlar. Aykırı verileri görerek, veri içindeki çeşitliliği daha iyi anlayabiliriz.
Standard Sapma
Matematiksel ifadeyle, varyansın karekökünü aldığımızda standart sapmaya ulaşırız. Veri biliminde standart sapmanın gösterdiği değer, verilerimizin aritmetik ortalama etrafında ne şekilde değiştiğini ifade eder. Standard sapma ayrıca, size ilerde anlatacağım istatistik testlerinde kullanılan önemli bir metriktir.
import statistics as st
st.variance(satıs_list) # 19.923684210526314
st.stdev(satıs_list) # 4.463595435355484
# st.pvariance() Evren/Population için kullanılırFrekans
Veri setinin içindeki verilerin, belirli aralıklar dahilinde ne kadar bulunduğunu hesaplamak için kullanılır. Örnek verecek olursak, şöyle bir veri setimiz olsun;
hist_data = [1,9,22,24,32,33,42,44,57,66,70,73,75,76,79,82,87,89,95,100]ve aralıklar da şöyle belirlenmiş olsun;
1-21, 21-41, 41-61, 61-81, 81-101
Kolları sıvayıp, Python‘da belirli bir aralık için frekans bulma fonksiyonu yazalım.
def frekans_hesapla(list_ex, min, max):
ctr = 0
for x in list_ex:
if min <= x <= max:
ctr += 1
return ctrVeri setimiz için fonksiyonu uygulayıp sonuçları çıkaralım.
frekans_hesapla(hist_data, 1, 21) # 2
frekans_hesapla(hist_data, 21, 41) # 4
frekans_hesapla(hist_data, 41, 61) # 3
frekans_hesapla(hist_data, 61, 81) # 6
frekans_hesapla(hist_data, 81, 101) # 5Histogram
Yukarıda hesapladığımız frekans değerlerini bir grafik üzerinde gösterdiğimizde histogramımızı elde etmiş oluruz. Histogram kısaca, gruplandırılmış verinin sütun grafik üzerinde gösterimidir. Yukarıda değerleri Python ile grafikte gösterecek olursak;
import matplotlib.pyplot as plt
hist_data = [1,9,22,24,32,33,42,44,57,66,70,73,75,76,79,82,87,89,95,100]
plt.hist(hist_data, bins=5) # bins için aralık sayısını seçmelisiniz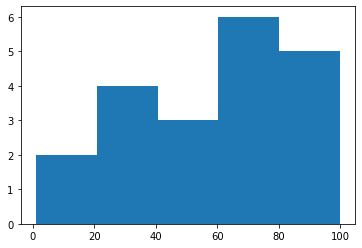
Bu arada yukarıdaki mean, standart sapma gibi metrikleri pandas’ın describe fonksiyonuyla da çıkarabilirsiniz.
Bir sonraki yazıda görüşmek üzere!
Kalın sağlıcakla!